Skip to contents

PCHA

2025-05-06

pcha.Rmd

Overview of PCHA implemented in Rust

1. Problem set-up

symbol shape meaning
X∈ℝp×nX\in\mathbb{R}^{p\times n} variables × samples raw data
I⊆{1,…,n}I\subseteq\{1,\dots,n\} (I=n_I) dictionary columns (“atoms”)
U⊆{1,…,n}U\subseteq\{1,\dots,n\} (U=n_U) columns to be approximated
kk — number of archetypes (components)

We split X=[XIXI‾]X = [\,X_I\;X_{\,\bar I}\,] and seek

XU≈XI⏟p×nIC⏟nI×kS⏟k×nU \boxed{\;X_U\;\approx\;\underbrace{X_I}_{p\times n_I}\; \underbrace{C}_{n_I\times k}\; \underbrace{S}_{k\times n_U}\;}

with the convex-hull constraints

C≥0,S≥0,∥S:,j∥1=1,∥C:,t∥1≈1(±δ). C\ge 0,\quad S\ge 0,\qquad \|S_{:,j}\|_{1}=1,\quad \|C_{:,t}\|_{1}\approx 1\;(\pm\delta).

The sum-of-squares error (SSE) to minimise is

SSE(C,S)=∥XU−XICS∥F2. \mathrm{SSE}(C,S)= \|X_U-X_I C S\|_F^{2}. \tag{1}

2. Algebra that drives the code

  1. Expand (1)

    ∥A−B∥F2=tr((A−B)⊤(A−B))=∥XU∥F2−2tr(S⊤C⊤XI⊤XU)+tr(S⊤C⊤XI⊤XICS). \begin{aligned} \|A-B\|_F^{2} &=\operatorname{tr}\bigl((A-B)^\top(A-B)\bigr) \\ &=\|X_U\|_F^{2} -2\,\operatorname{tr}\!\bigl(S^\top C^\top X_I^\top X_U\bigr) +\operatorname{tr}\!\bigl(S^\top C^\top X_I^\top X_I C S\bigr). \end{aligned}

    Two cached Gram matrices therefore appear everywhere in the Rust code

    G:=XI⊤XU,H:=XI⊤XI. G := X_I^\top X_U,\qquad H := X_I^\top X_I.

  2. Gradients

    ∇SSSE=(C⊤HC)S−C⊤G,∇CSSE=HC(SS⊤)−GS⊤. \nabla_S\mathrm{SSE} = (C^\top H C)\,S - C^\top G, \quad \nabla_C\mathrm{SSE} = H\,C\,\bigl(SS^\top\bigr)-G S^\top .

    (These two lines are the heart of s_update and c_update.)

  3. Projected–gradient step

    • Take a gradient step: Z←Y−μ∇YZ\leftarrow Y - \mu\,\nabla_Y for Y∈{C,S}Y\in\{C,S\}.

    • Project back to the feasible set. Each column is sent onto the probability simplex

      $$ \Delta^{m-1}:=\Bigl\{\,z\in\mathbb{R}^m_{\ge 0}: \langle\mathbf 1,z\rangle=1\Bigr\}, $$

      using the Wang–Carreira-Perpiñán algorithm (O(m log m)), implemented in project_simplex.

    • Armijo-type line-search If the new SSE is not smaller, shrink μ:=μ/2\mu:=\mu/2; else accept and enlarge μ:=1.2μ\mu:=1.2\,\mu. (see the inner while !stop loops).

  4. Optional “α-relaxation’’ To let each archetype deviate slightly from exact $ _1! =!1$, a per-column scalar αt∈[1−δ,1+δ]\alpha_t\in[1-\delta,\,1+\delta] is fitted (second part of c_update). In formulas: minimise w.r.t. α\alpha

    ∥XU−XI(Cdiagα)S∥F2. \|\,X_U - X_I\,(C\operatorname{diag}\alpha)\,S\|_F^{2}.

3. Initialisation

  • Furthest-Sum (FS) finds kk columns of XIX_I that are mutually far apart in Euclidean distance:

    choose seed  i₁
repeat
      pick   i_{t+1} := argmax_j Σ_{s≤t} ‖x_{i_s}-x_j‖

    FS provides an indicator matrix C(0)C^{(0)} with exact simplex columns (one “1” each).

  • Dirichlet-type random S(0)S^{(0)} Each column is drawn i.i.d. from Dirichlet(𝟏)\operatorname{Dirichlet}(\mathbf 1) ⇒ uniform over the simplex.

4. Stopping rule

Iterate until

|SSE(t−1)−SSE(t)|SSE(t)<tolorSSE(t)∥XU∥F2>1−ε(≈ 99.99 % var. expl.) \frac{|\mathrm{SSE}^{(t-1)}-\mathrm{SSE}^{(t)}|} {\mathrm{SSE}^{(t)}} <\text{tol} \quad\text{or}\quad \frac{\mathrm{SSE}^{(t)}}{\|X_U\|_F^{2}} > 1-\varepsilon\;(\text{≈ 99.99 % var. expl.})

or the iteration cap is hit (default 750).

5. Output

  • CC and SS re-ordered by column usage ut=∑jStju_t=\sum_j S_{tj} (desc).
  • Archetypes XC=XICXC = X_I C.
  • Final SSE and variance explained VarExpl=1−SSE/∥XU∥F2\mathrm{VarExpl}=1-\mathrm{SSE}/\|X_U\|_F^{2}.

Create a data set with a known archetypal structure 

library(rustytools)
### Toy data with a known archetypal structure
set.seed(42)
p  <- 60            # genes
n  <- 300           # cells
k0 <- 5             # ground-truth archetypes

# 1. ground-truth archetype matrix A (p × k0)
A <- matrix(rexp(p * k0, 1), p, k0)
# 2. sample coefficients S on the simplex
alpha <- matrix(rexp(k0 * n, 1), k0, n)
S     <- sweep(alpha, 2, colSums(alpha), "/")
# 3. generate data with small noise
X <- A %*% S + matrix(rgamma(p * n, shape = 1, rate = 50), p, n)

Finding optimal number of archetypes

First we set a number of k to iterate through. Using the future library we can perform pcha on each k in parallel. We normalize the sum squared error, then use the find_knee_pt function to find the optimal number of archetypes which is our ground truth archetype from above

ks <- 1:10
sse <- sapply(ks, function(k) pcha(X, k)$sse)
norm_sse  <- sse / sum(X * X)                           
kp   <- find_knee_pt(norm_sse, ks, make_plot = TRUE)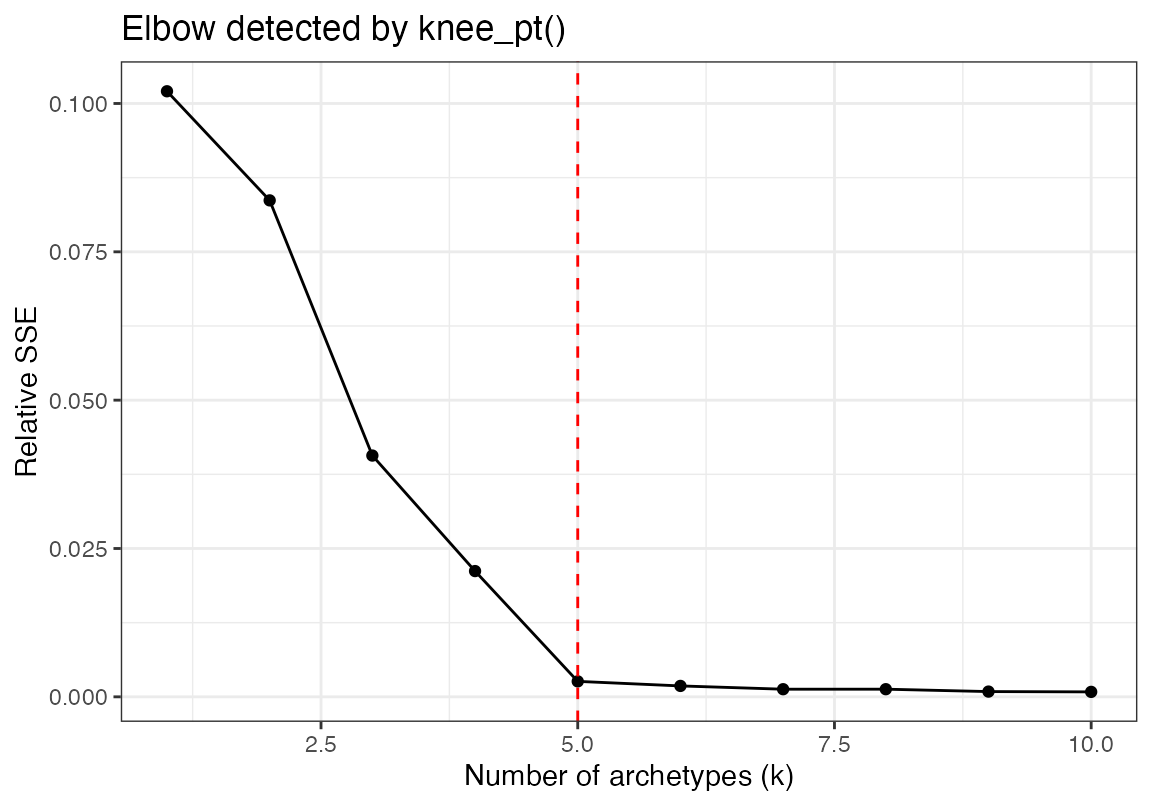

cat("Optimal number of archetypes =", kp$knee_x, "\n")
## Optimal number of archetypes = 5

What does this look like in single cell RNA sequencing data

First subset out the tumor

library(Seurat)
library(ggplot2)
library(scCustomize)
library(magrittr)

seu <- readRDS("~/Fred Hutch Cancer Center/Furlan_Lab - General/experiments/patient_marrows/annon/AML101/aml101.cds")
DimPlot(seu, group.by = "seurat_clusters")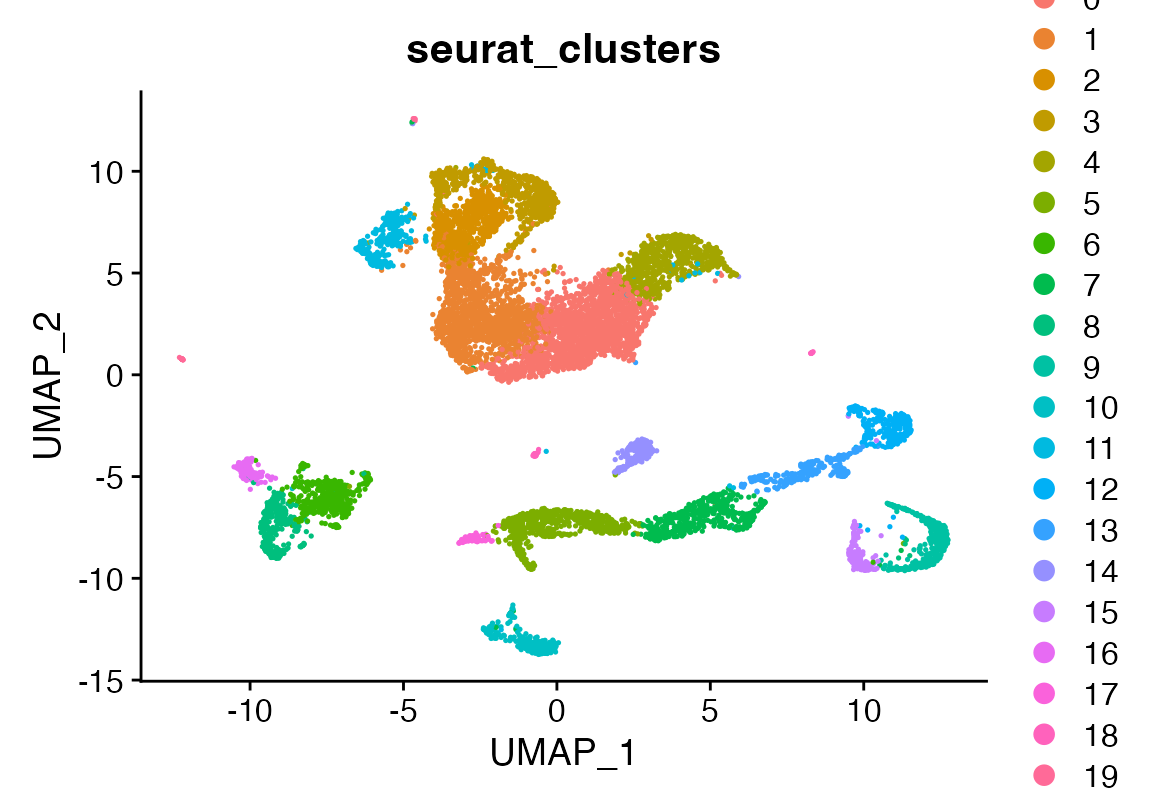

DimPlot(seu, group.by = "geno")

seu$sb <- seu$geno %in% "0" & seu$seurat_clusters %in% c("0", "1", "2", "3", "4", "11")
seu <- seu[,seu$sb]
seu <- NormalizeData(seu, verbose = F) %>% ScaleData(verbose = F) %>% FindVariableFeatures(verbose = F) %>% RunPCA(npcs = 100, verbose = F)
ElbowPlot(seu, ndims = 100)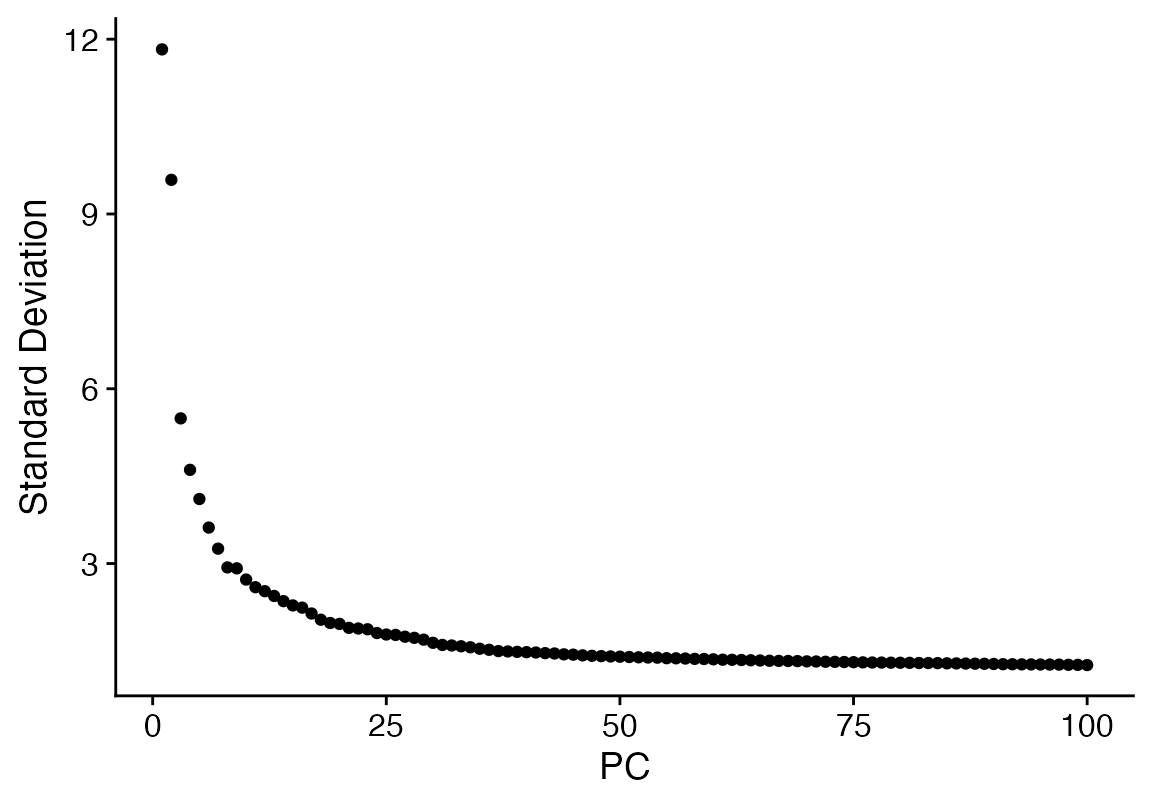

seu <- FindNeighbors(seu, dims = 1:35, verbose = F) %>% FindClusters(verbose = F) %>% RunUMAP(dims = 1:35, n.epochs = 500, verbose = F)
DimPlot(seu)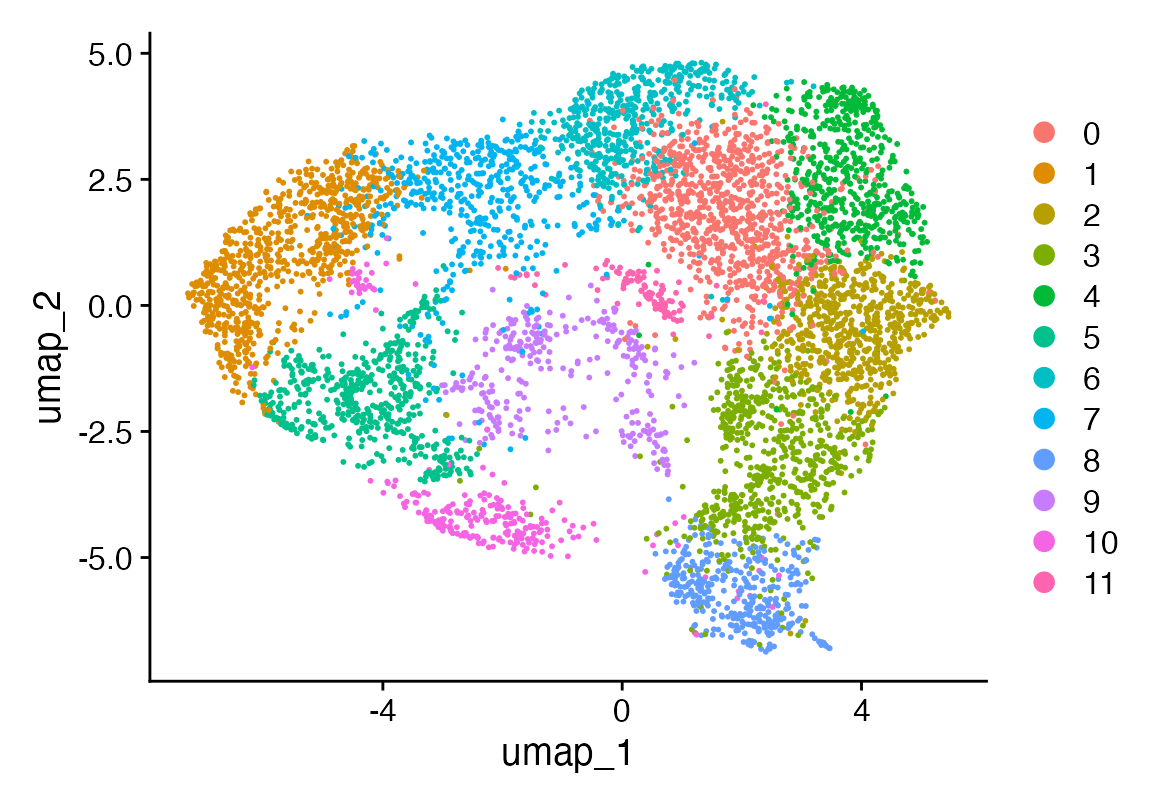

Use some magic.

seu <- seurat_magic(seu, alpha = 1)
DefaultAssay(seu) <- "MAGIC"
seu <- NormalizeData(seu, assay = "MAGIC") %>% ScaleData(verbose = F) %>% FindVariableFeatures(nfeatures = 5000, assay = "MAGIC", verbose = F) %>%  RunPCA(assay = "MAGIC", npcs = 100, verbose = F)

Find nuber of PCs that correspond to 85% of variance

# pull out the per‐PC standard deviations (as before)
sdev <- seu@reductions$pca@stdev

# compute the % variance explained by each PC
explained_var <- sdev^2 / sum(sdev^2)

# cumulative sum
cum_var <- cumsum(explained_var)

# find the first PC where cumulative ≥ 0.85
pct_cutoff <- 0.85
n_pc_85 <- which(cum_var >= pct_cutoff)[1]

message("Using ", n_pc_85, " PCs, which explain ",
        round(100 * cum_var[n_pc_85], 1), "% of variance.\n")

# now subset your cell×PC matrix
pcs_85 <- Embeddings(seu, "pca")[, 1:n_pc_85, drop = FALSE]

seu <- FindNeighbors(seu, dims = 1:n_pc_85, verbose = F, k.param = 5) %>% FindClusters(verbose = F) %>% RunUMAP(dims = 1:n_pc_85, n.epochs = 500, verbose = F)
DimPlot(seu, reduction = "umap")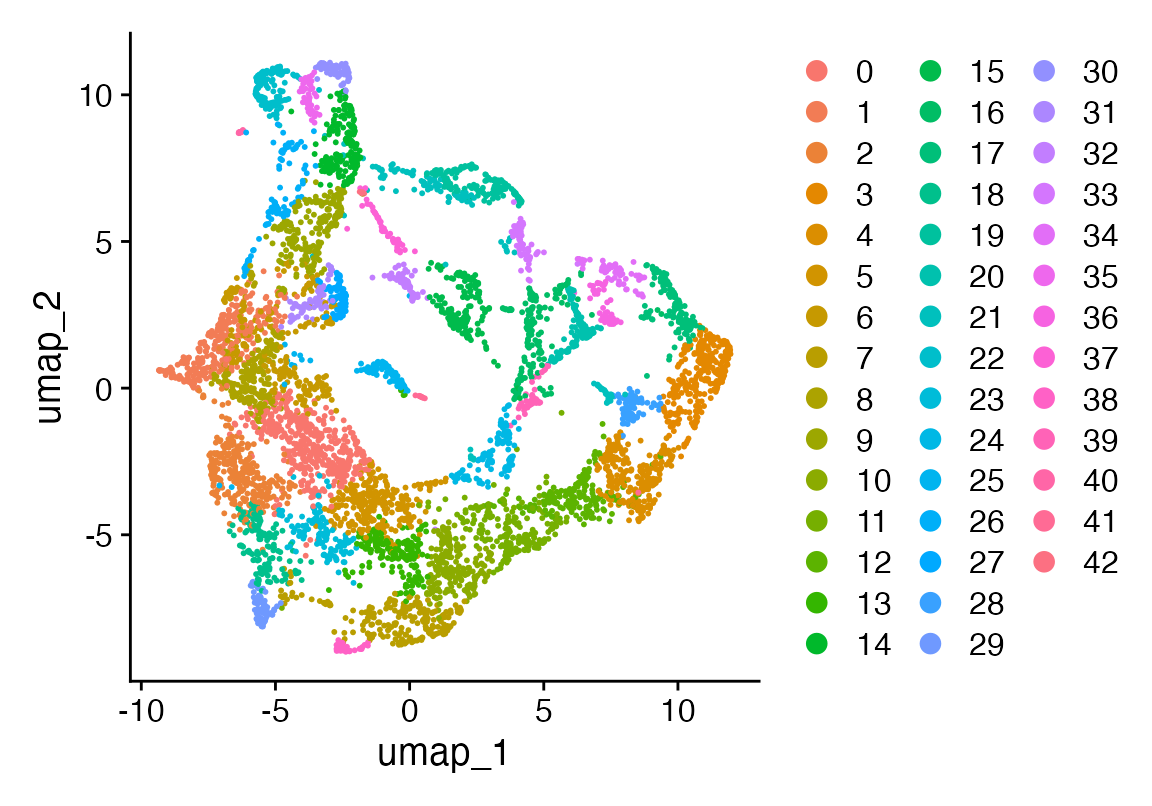

X <- as.matrix(t(seu@reductions$pca@cell.embeddings[,1:n_pc_85]))

Reproducibility

To ensure reproducibility we can pass random starts to the rust pcha implementation from R. Note that this is not necessary to do in normal practice. Because slightly different solutions may be found with each run of pcha given the random starts, using R to generate random starts is one way to ensure reproducibility. However, the random starts produced in Rust are adequate for most purposes. One suggestion would be to calculate multiple solutions using Rust random starts and use a consensus solution.

set.seed(123)

# ---- 1. implement furthest_sum in R, this is done in the Rust implementation natively ----
furthest_sum <- function(X, k, seed = NULL){
  # X: p×n data matrix (genes × cells), but we only care about columns here
  n <- ncol(X)
  # precompute squared norms
  norms2 <- colSums(X^2)
  # pick initial seed at random if not provided
  if (is.null(seed)) seed <- sample.int(n, 1)
  archetypes <- integer(k)
  archetypes[1] <- seed
  # maintain a running "sum of distances" for each column
  sum_dists <- numeric(n)
  picked <- logical(n)
  picked[seed] <- TRUE

  for (j in 2:k) {
    last <- archetypes[j - 1]
    # distances from last seed to all columns: sqrt(||x_i||^2 + ||x_last||^2 - 2 x_i·x_last)
    # we only need the sqrt to compare, but sum of sqrt is monotonic so we'll do it exactly:
    dots <- crossprod(X[, last], X)    # 1×n vector of dot products
    d2   <- norms2 + norms2[last] - 2 * as.numeric(dots)
    sum_dists[!picked] <- sum_dists[!picked] + sqrt(d2[!picked])
    # pick the column with max cumulative distance
    next_seed <- which.max(ifelse(picked, -Inf, sum_dists))
    archetypes[j] <- next_seed
    picked[next_seed] <- TRUE
  }
  archetypes
}


# ---- 2. build C0 and S0 ----
make_pcha_starts <- function(X, k, rng_seed = 1234, s_rng_seed = 5678){
  set.seed(rng_seed)
  seeds <- furthest_sum(X, k)
  # C0: n×k (because Rust's ni = #columns of X)
  C0 <- matrix(0, nrow = ncol(X), ncol = k)
  for (j in seq_len(k)) C0[seeds[j], j] <- 1

  # S0: k×n uniform → normalized columns
  set.seed(s_rng_seed)
  S0 <- matrix(runif(k * ncol(X)), nrow = k, ncol = ncol(X))
  S0 <- sweep(S0, 2, colSums(S0), "/")

  list(C0 = C0, S0 = S0)
}

kmax <- 15
ks  <- 1:kmax
starts <- lapply(ks, function(k){
  make_pcha_starts(X, k,
                   rng_seed   = 1000 + k,
                   s_rng_seed = 2000 + k)
})

sse  <- sapply(seq_along(ks), function(i){
  k  <- ks[i]
  C0 <- starts[[i]]$C0
  S0 <- starts[[i]]$S0
  message("running PCHA for k=", k, " …")
  pcha(X, k, c_init = C0, s_init = S0)$sse
})

norm_sse  <- sse / sum(X * X)                           
kp   <- find_knee_pt(norm_sse, ks, make_plot = TRUE)

cat("Optimal number of archetypes =", kp$knee_x, "\n")
## Optimal number of archetypes = 3
noc <- kp$knee_x
res <- pcha(X, noc) 
weights_df <- as.data.frame(t(res$S))     # cells × k
colnames(weights_df) <- paste0("arch", seq_len(noc))


# a single label: archetype with the largest weight
seu$max_arch <- factor(
  apply(weights_df, 1L, which.max),
  levels = seq_len(noc),
  labels = paste0("Arch", seq_len(noc))
)

DimPlot(seu, reduction = "umap", group.by = "max_arch")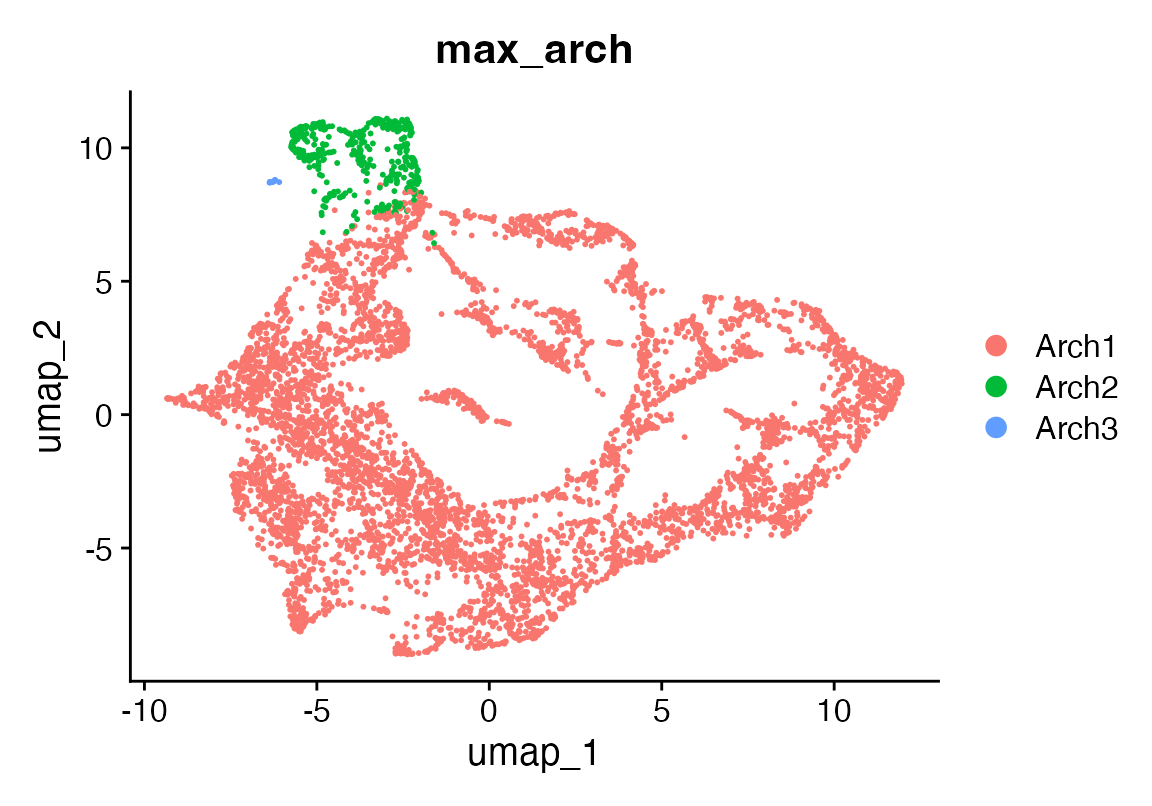

S_df <- as.data.frame(t(res$S))
colnames(S_df) <- paste0("Arch", seq_len(ncol(S_df)))

# 2) pick your “specialist” threshold
specialist_thresh <- 0.95


# 3) for each cell, find if its max-weight > threshold; if so, label by archetype
max_w   <- apply(S_df, 1, max)
best_k  <- apply(S_df, 1, which.max)
specialist_label <- ifelse(max_w > specialist_thresh,
                           paste0("Arch", best_k),
                           NA_character_)

# 4) add to Seurat
seu$specialist <- specialist_label


p <- DimPlot(seu, reduction = "umap", group.by = "specialist")
p + scale_colour_discrete(na.value = "lightgrey")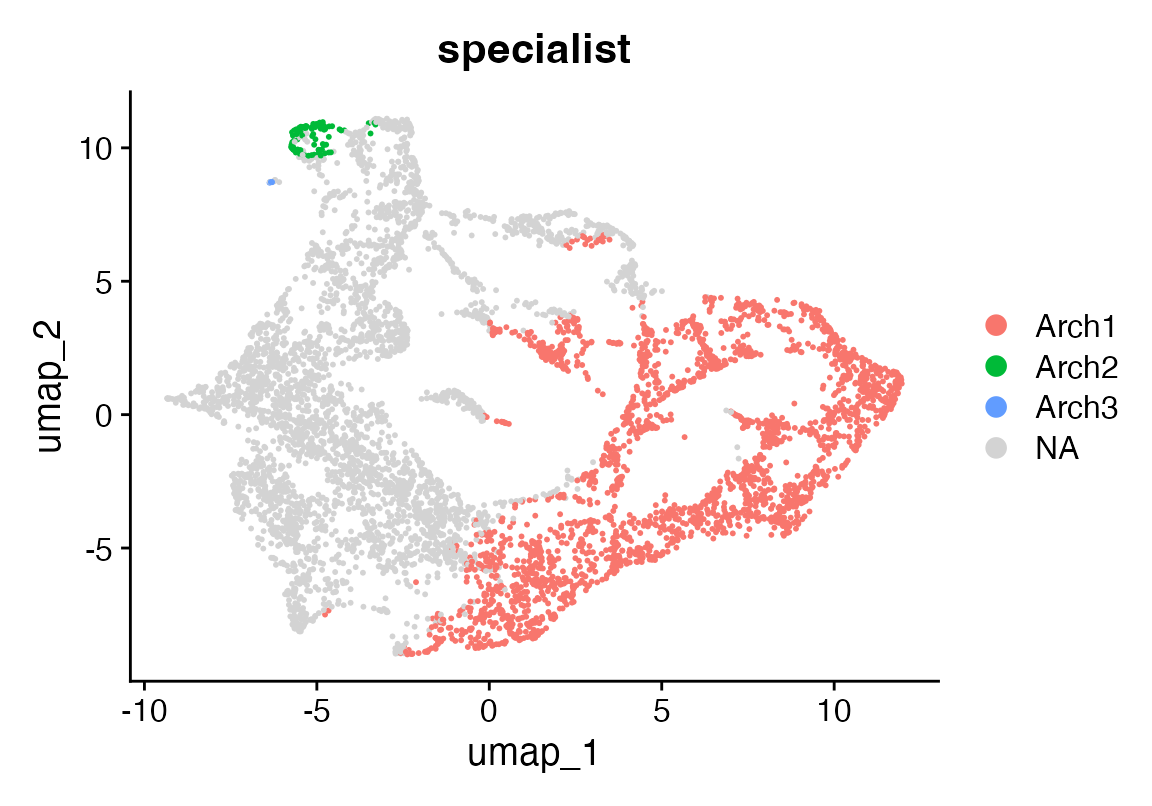

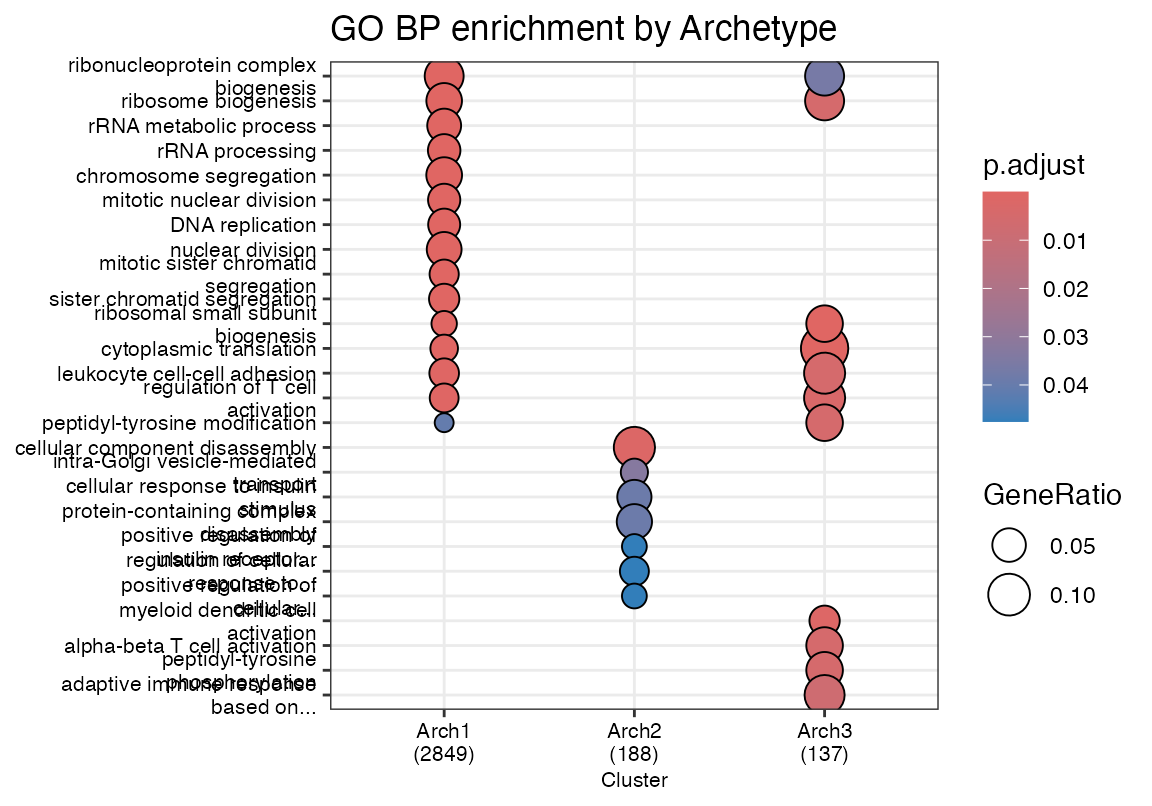
Pathway analysis of archetype specialists 

suppressPackageStartupMessages({library(dplyr)
library(purrr)
library(clusterProfiler)
library(org.Hs.eg.db)})

DefaultAssay(seu)<- "RNA"
seu_spec <-seu[,!is.na(seu$specialist)]
# 1) For each archetype, find a “marker gene list” (here: top 200 avg. expr)
marker_genes <- FindAllMarkers(seu_spec, group.by = "specialist", )
marker_genes$diff <- abs(marker_genes$pct.1 - marker_genes$pct.2)

marker_genes_filt <- marker_genes[marker_genes$p_val_adj<5e-2 & abs(marker_genes$avg_log2FC) > 1 & marker_genes$diff>0.1,]

marker_genes_filt <- marker_genes_filt[!duplicated(marker_genes_filt$gene),]

ccr <- compareCluster(
  gene ~ cluster,
  data         = marker_genes_filt,
  fun          = "enrichGO",
  OrgDb        = org.Hs.eg.db,
  keyType      = "SYMBOL",
  ont          = "BP",
  pAdjustMethod= "BH",
  pvalueCutoff = 0.05,
  qvalueCutoff = 0.05,
  readable     = TRUE
)

# fix length of terms...
shorten_terms <- function(terms, max_words = Inf, max_chars = Inf) {
  sapply(terms, function(term) {
    words <- strsplit(term, "\\s+")[[1]]
    truncated <- term
    did_trunc <- FALSE
    
    if (!is.infinite(max_words) && length(words) > max_words) {
      truncated <- paste(words[1:max_words], collapse = " ")
      did_trunc <- TRUE
    }
    
    if (!is.infinite(max_chars) && nchar(truncated) > max_chars) {
      cut_sub <- substr(truncated, 1, max_chars)
      spaces <- gregexpr("\\s+", cut_sub)[[1]]
      if (all(spaces == -1)) {
        truncated <- cut_sub
      } else {
        last_space <- tail(spaces, 1)
        truncated <- substr(cut_sub, 1, last_space - 1)
      }
      did_trunc <- TRUE
    }
    
    if (did_trunc) truncated <- paste0(truncated, "...")
    truncated
  }, USE.NAMES = FALSE)
}

ccr@compareClusterResult$Description <- shorten_terms(ccr@compareClusterResult$Description, max_chars = 40)

dotplot(ccr, showCategory=10, font.size = 8) + ggtitle("GO BP enrichment by Archetype")