Skip to contents

Magic in R and Rust

2025-05-06

magic.Rmd

Overview of Magic implemented in R and Rust

(“Markov Affinity-based Graph Imputation of Cells” – van Dijk et al., 2018)

Symbol Size Meaning
X n × g raw (or PCA-reduced) expression; rows = cells, cols = genes
d(i,j) – Euclidean (or cosine) distance between cell i and j in PCA space
σᵢ – local scale for cell i (distance to its k-th nearest neighbour)
A n × n symmetrised, locally scaled affinity (“heat”) matrix
D n × n diagonal degree matrix, Dii = ∑jAij
P = D⁻¹A n × n row-stochastic Markov transition matrix
t – diffusion time (walk length)
Ŷ n × g imputed expression after diffusion

1 k-NN graph in latent space

Compute k nearest neighbours in the m-dimensional PCA space (typically k ≈ 30, m ≈ 100).

This is done by Seurat or related packages.

2 Adaptive Gaussian kernel

For each edge (i, j) in that graph set

$$ A_{ij} \;=\; \begin{cases} \displaystyle \exp\!\Bigl(-\frac{d(i,j)^2}{\sigma_i\,\sigma_j}\Bigr), & j\in\mathrm{kNN}(i),\\[6pt] 0, & \text{otherwise.} \end{cases} $$

Local bandwidths σᵢ make the kernel anisotropic so dense and sparse regions of the manifold are treated equally.

Symmetrise

A←12(A+A⊤) A \;←\; \tfrac12\,(A + A^{\!\top})

3 Markov normalisation

P=D−1A,Dii=∑jAij. P \;=\; D^{-1}A, \quad D_{ii} = \sum_{j} A_{ij}.

Now each row of P sums to 1 → one step of a random walk on the cell graph.

This is done in R:

row_sums <- Matrix::rowSums(A)
P <- Matrix::Diagonal(x = 1 / pmax(row_sums, 1e-12)) %*% A

4 Diffusion (raise to power t)

There are two equivalent views:

  • Spectral Diagonalise P = Ψ Λ Ψ⁻¹ with eigenvalues 1 = λ₀ > λ₁ ≥ λ₂ … Then

    Pt=ΨΛtΨ−1,Λt=diag(λkt). P^{t} \;=\; \Psi\,\Lambda^{t}\,\Psi^{-1}, \qquad \Lambda^{t} = \operatorname{diag}(\lambda_k^{t}).

    Small eigenmodes (high-frequency noise) decay as λₖᵗ.

  • Random-walk Entry (i,j) of Pᵗ is the probability that a random walk of length t starting at cell i ends in cell j.

5 Imputation by heat propagation

Apply the diffusion operator to every gene vector:

X̂=PtX⇒x̂ig=∑j=1n(Pt)ijxjg. \boxed{\; \hat X = P^{t}\,X \;} \quad\Longrightarrow\quad \hat x_{ig} = \sum_{j=1}^{n} (P^{t})_{ij}\; x_{jg}.

Each imputed expression value becomes a weighted average over the t-step neighbourhood, smoothing drop-outs while respecting manifold structure.

Relation to the continuous heat equation

On a smooth data manifold M, the generator L = I – P approximates the Laplace–Beltrami operator ΔM. Diffusion time t therefore controls how far one solves the heat-equation

∂u∂t=−ΔMu,u(0)=X. \frac{\partial u}{\partial t} \;=\; -\Delta_M\,u, \qquad u(0)=X.

MAGIC performs this on a graph and stops at a user-chosen t (often 2–6); too small → little denoising, too large → over-smoothing.

Blended MAGIC imputation

We have added an additional lever which controls the strength of the diffusion process.

Let

  • X∈ℝn×gX\in\mathbb{R}^{n\times g} be the original (cells × genes) expression matrix,
  • P∈ℝn×nP\in\mathbb{R}^{n\times n} the row-stochastic diffusion operator,
  • t∈ℕt\in\mathbb{N} the number of diffusion steps,
  • X̃=PtX\widetilde X = P^{\,t} X the fully-diffused matrix,
  • α∈[0,1]\alpha\in[0,1] the blending weight.

We define the blended imputation

$$ X_{\rm imp}(\alpha) \;=\; (1 - \alpha)\,X \;+\; \alpha\,\widetilde X \;=\; (1 - \alpha)\,X \;+\; \alpha\,P^{\,t}\,X \;\in\mathbb{R}^{n\times g}. $$

Special cases

$$ \begin{aligned} \alpha = 0:\quad &X_{\rm imp}(0) = X,\\ \alpha = 1:\quad &X_{\rm imp}(1) = P^{t}X,\\ 0 < \alpha < 1:\quad &\text{Partial smoothing (convex blend of $X$ and $P^{t}X$).} \end{aligned} $$

Per-entry formula

For each cell ii and gene jj:

$$ X_{\rm imp}^{(i,j)}(\alpha) \;=\;(1 - \alpha)\,X^{(i,j)} \;+\;\alpha\sum_{k=1}^{n} \bigl[P^{\,t}\bigr]_{ik}\,X^{(k,j)}. $$

Interpretation

  • α\alpha directly controls the strength of smoothing:

    • Small α\alpha preserves more of the raw, per-cell expression.
    • Large α\alpha favors neighborhood-averaged values.

  • Choosing α\alpha between 0 and 1 lets you trade off noise reduction vs. signal fidelity without changing tt or the underlying graph.

How to run MAGIC in R/Rust

First we take some data, subset to the tumor cells that express modest levels of CD33.

suppressPackageStartupMessages({
  library(Seurat)
  library(scCustomize)
  library(rustytools)
  library(magrittr)
})


seu <- readRDS("~/Fred Hutch Cancer Center/Furlan_Lab - General/experiments/patient_marrows/annon/AML101/aml101.cds")
seu$sb <- seu$geno %in% "0" & seu$seurat_clusters %in% c("0", "1", "2", "3", "4", "11")
seu <- seu[,seu$sb]
seu <- NormalizeData(seu, verbose = F) %>% ScaleData(verbose = F) %>% FindVariableFeatures(verbose = F) %>% RunPCA(npcs = 100, verbose = F)
ElbowPlot(seu, ndims = 100)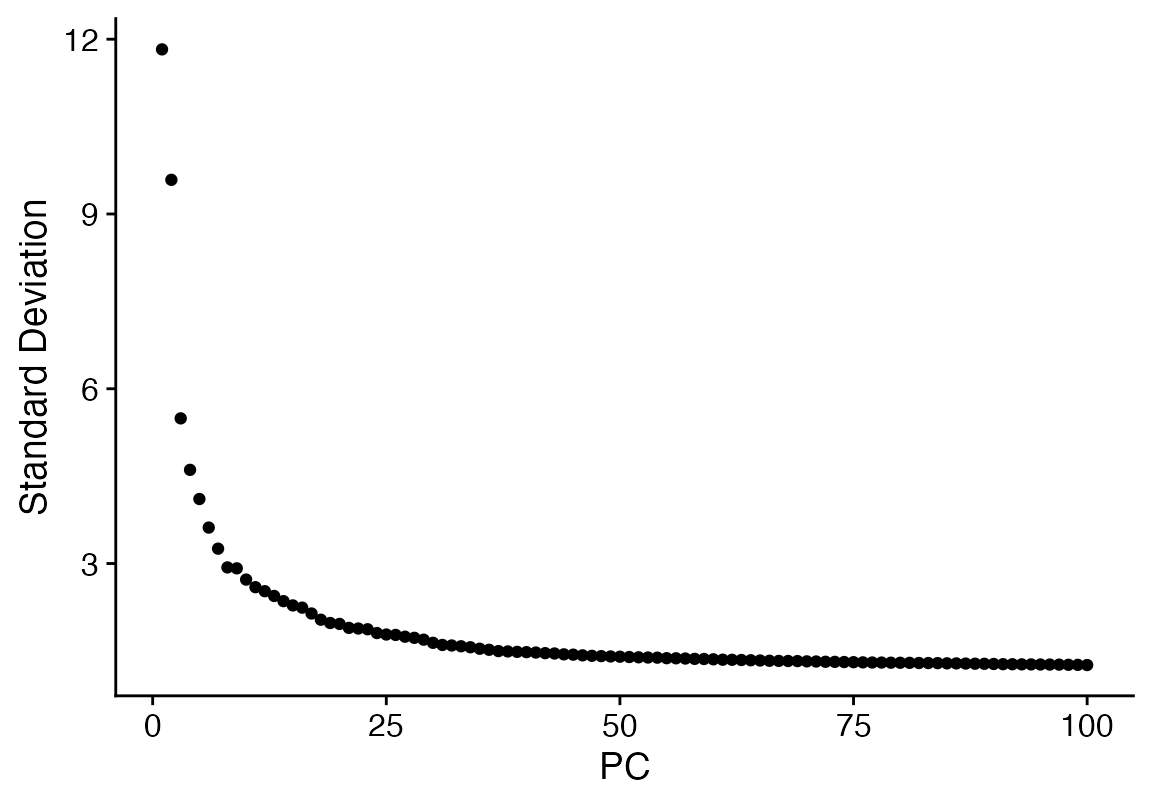

seu <- FindNeighbors(seu, dims = 1:35, verbose = F) %>% FindClusters(verbose = F) %>% RunUMAP(dims = 1:35, n.epochs = 500, verbose = F)
DimPlot(seu)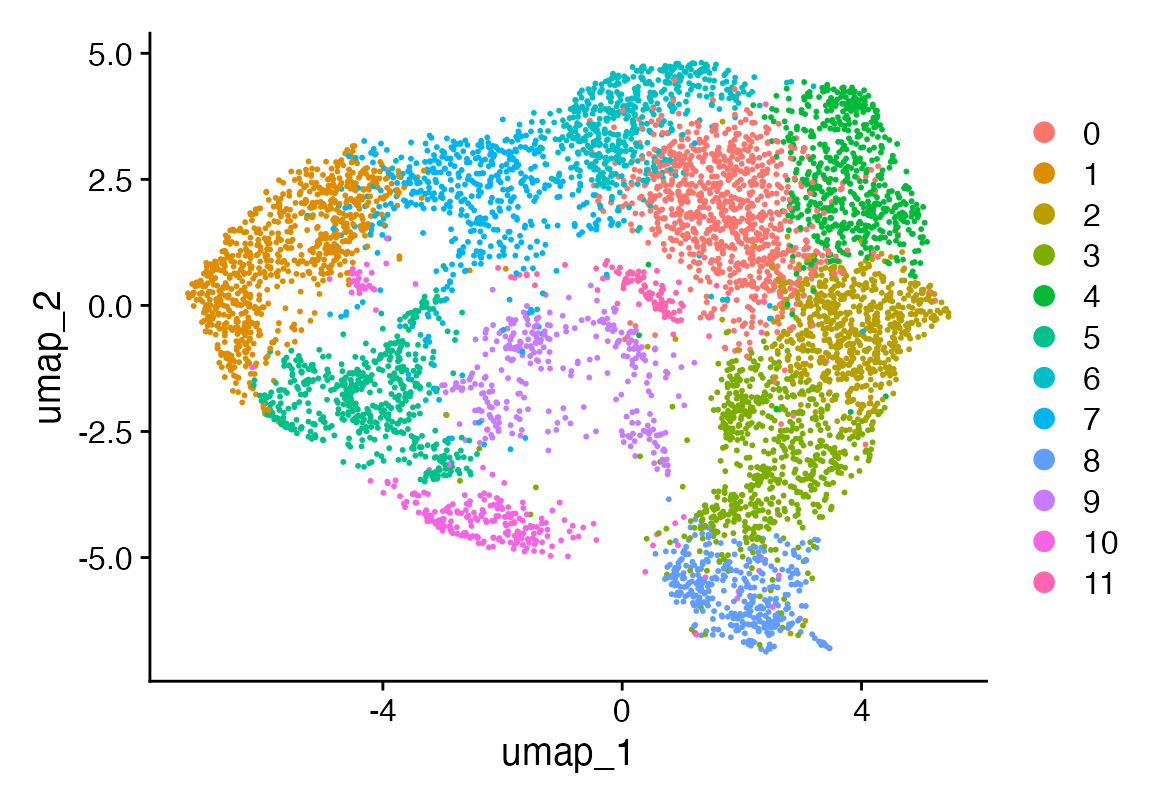

DefaultAssay(seu) <- "RNA"
FeaturePlot_scCustom(seu, "CD33")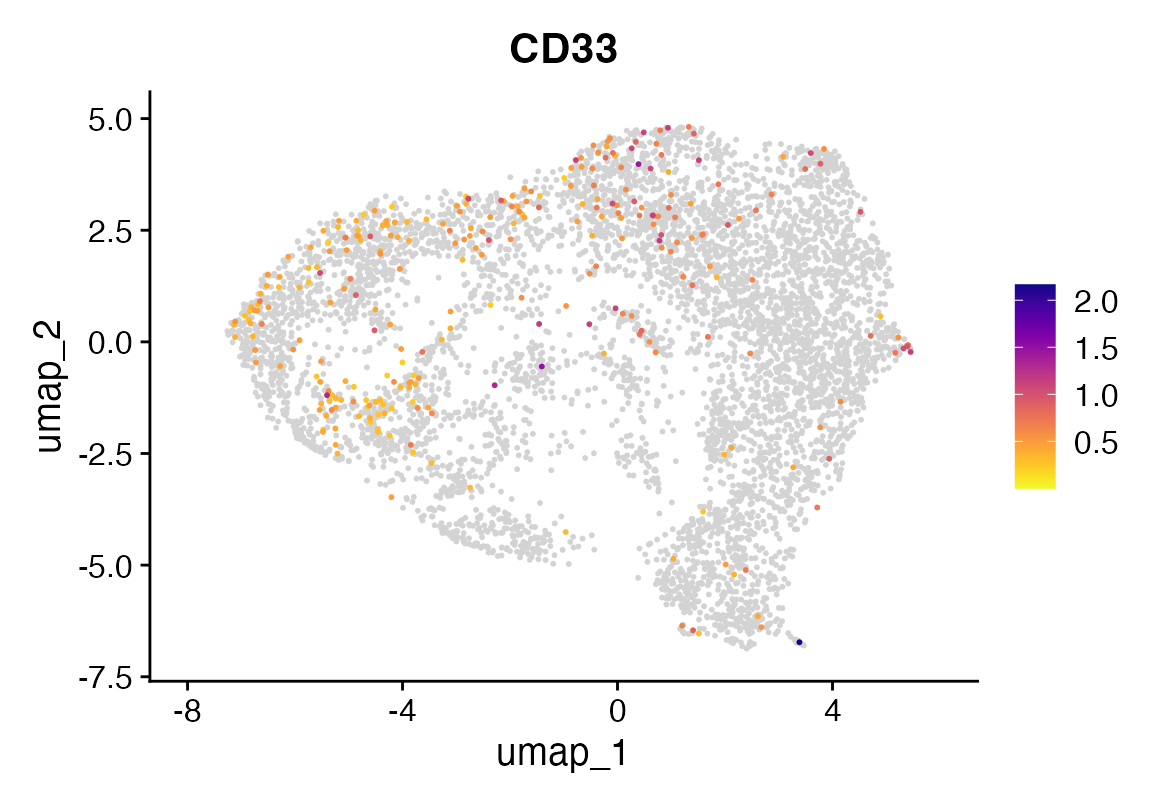

Now let’s see how they look after some magic.

seu <- seurat_magic(seu, alpha = 1)
DefaultAssay(seu) <- "MAGIC"
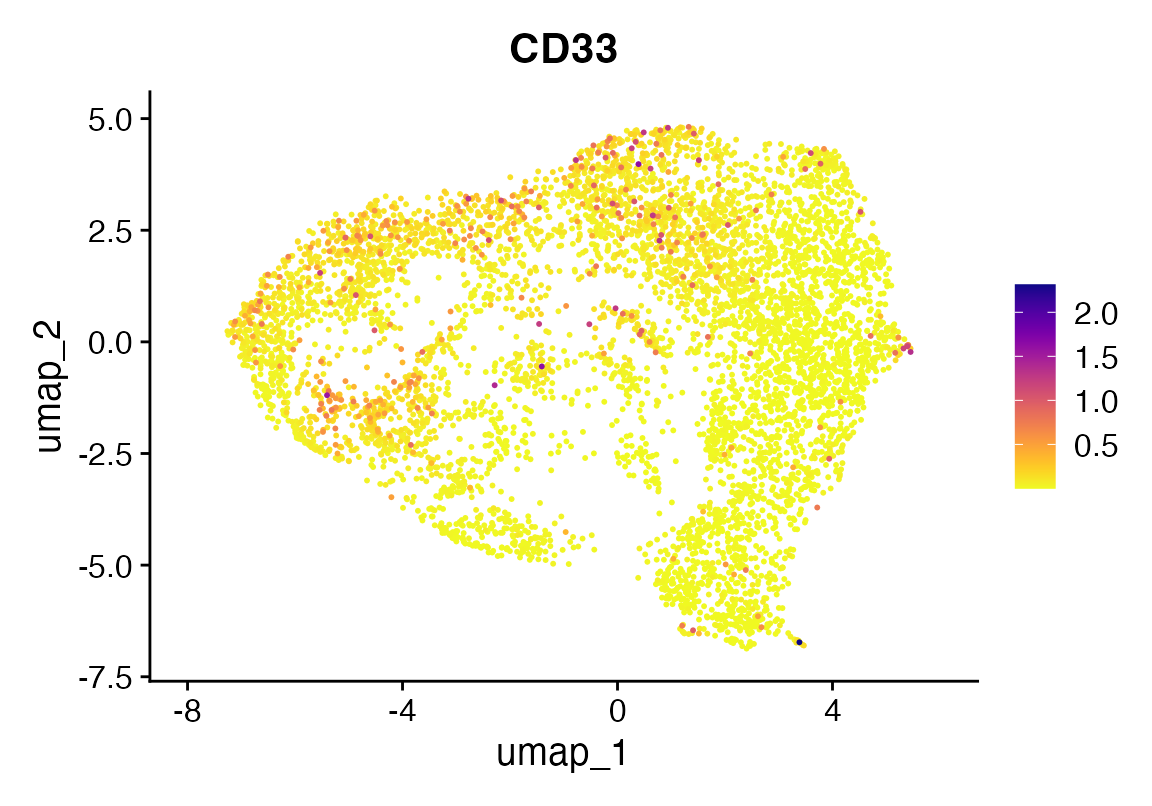
FeaturePlot_scCustom(seu, "CD33")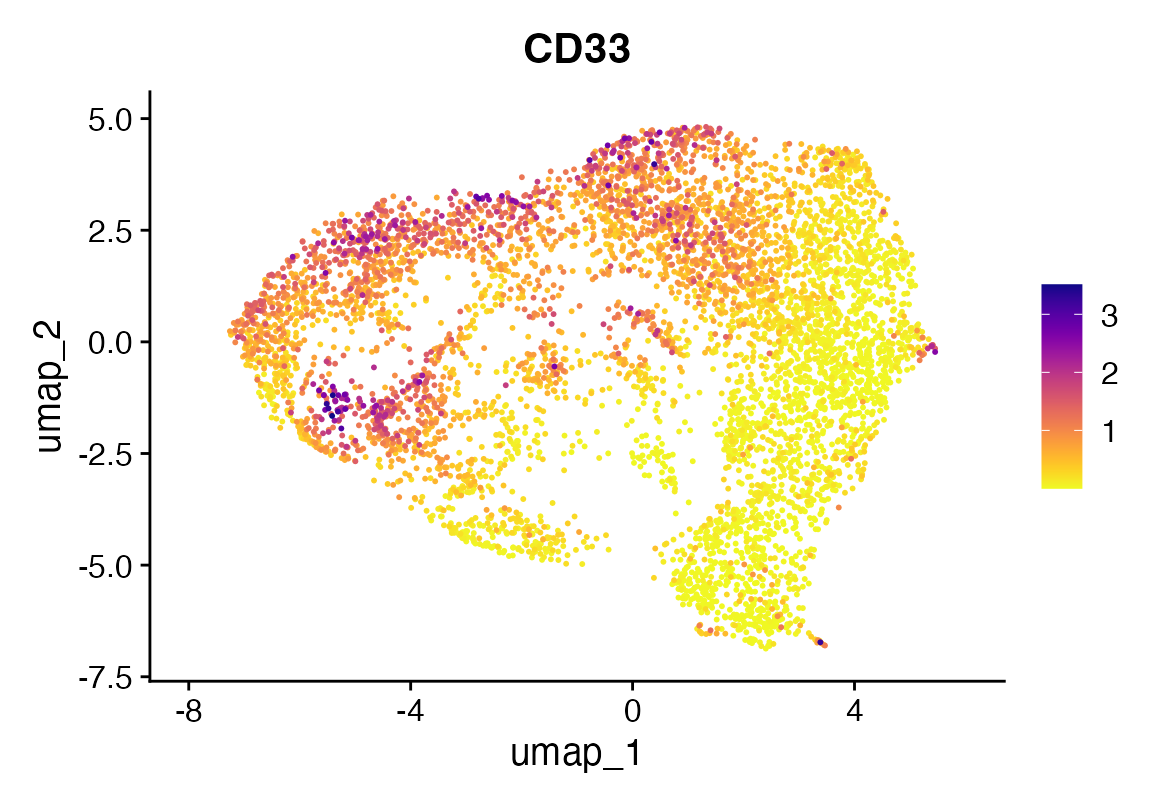

Changing parameters

An alpha of 1 might be too much. We can dial it back with an alpha of 0.3 and even further by dropping t to 2.

seu <- seurat_magic(seu, alpha = 0.3)

DefaultAssay(seu) <- "MAGIC"
FeaturePlot_scCustom(seu, "CD33")

seu <- seurat_magic(seu, alpha = 0.3, t = 2)

DefaultAssay(seu) <- "MAGIC"
FeaturePlot_scCustom(seu, "CD33")